Fraccionarios

Fraccionarios

1. NÚMEROS FRACCIONARIOS (Antes Quebrados) 3 4 Numerador Denominador Se lee tres cuartos El denominador indica las partes en que se divide la unidad; mientras el numerador, las partes que tomamos Gráficamente, la fracción sería: De un metro dividido en cuatro partes Tomamos tres partes Un número fraccionario es una división sin efectuar. Ejemplo:
2. 1 2 NÚMEROS FRACCIONARIOS Nomenclatura: Para leer un fracción se lee el numerador y, posteriormente, el denominador, pero con la siguiente nombre: A partir de 11 se lee el número y se le añade la terminación avos: 1 3 1 4 1 6 1 5 1 7 1 10 1 11 1 8 1 9 Un medio Un tercio Un cuarto Un quinto Un sexto Un séptimo Un octavo Un noveno Un décimo Un onceavos
3. NÚMEROS FRACCIONARIOS Clases de Fracciones: Propias: Cuando el numerador es menor que el denominador Igual a la unidad: Cuando el numerador es igual al denominador Impropias: Cuando el numerador es mayor que el denominador 3 4 3 3 3 2
4. 6 12 2 4 NÚMEROS FRACCIONARIOS Fracciones equivalentes Son aquellas que multiplicadas en cruz dan el mismo resultado. Ejemplo: 3 4 6 8 3 * 8 = 6 * 4 = Para averiguar fracciones equivalentes a una fracción dada, se multiplica o se divide el numerador y denominador por un mismo número. Ejemplo: buscar tres fracciones equivalentes a: x 2 = 4 8 x 3 = : 2 = 1 2 Cuatro octavos Seis doceavos Un medio
5. NÚMEROS FRACCIONARIOS Hallar una fracción de una cantidad . Para hallar una fracción de una cantidad, se divide la cantidad entre el denominador y el resultado se multiplica por el numerador. Ejemplos: Hallar una fracción de ¾ de la cantidad de 1.840 * 3; 1.840 4 x = x = 460 * 3; x = 1.380 Hallar una fracción de 3/5 de la cantidad de 2.840 x = 2.840 5 * 3; x = 568 * 3; x = 1.704
6. NÚMEROS FRACCIONARIOS Para sumar fracciones con igual denominador se coloca como denominador el mismo que lleva las fracciones y como numerador la suma de todos los numeradores. Suma de Fracciones a) Fracciones con igual denominador 3 5 2 5 6 5 + + = 4 7 1 7 3 7 1 5 8 7 + + =
7. NÚMEROS FRACCIONARIOS Suma de Fracciones b) Fracciones con distinto denominador Para sumar fracciones con distinto denominador hay que buscar otras tantas fracciones con igual denominador el cual sería el mínimo común múltiplo de los denominadores. Pasando a la opción a). Se divide el mismo denominador por cada denominador anterior y se multiplica por cada numerador anterior para hallar los nuevos numeradores. 2 9 1 8 2 5 + + ; m.c.m de 9, 8 y 5 = 360 360/9*2 360 + 360/8*1 360 360/5*2 360 + = 269 360 ; 80 360 + 45 360 + 144 360 = 80+45+144 360
8. NÚMEROS FRACCIONARIOS Problema De un depósito de 240 litros de agua hacemos tres extracciones. En la 1ª se saca 1/3 del total; en la 2ª, 2/5 del total; y en la 3ª, 2/9. ¿Qué fracción se ha sacado? ¿Qué fracción queda por sacar? 1 3 + 2 5 2 9 + m.c.m de 3, 5 y 9 = 45 15 45 + 18 45 10 45 + = 43 45 Fracción que se ha sacado 43 45 _ 2 45 45 45 = Fracción que queda por sacar
9. NÚMEROS FRACCIONARIOS Resta de Fracciones El procedimiento es el mismo de la suma, con la diferencia de que al primer numerador se le van restando los demás numeradores. Recordamos que para hallar el m.c.m. de varios números, se descomponen en factores primos; se pasa a forma de potencia y se toman uno de cada factor distinto con el mayor exponente. (Ver presentación de m.c.m. y m.c.d.) 7 8 1 6 1 4 21 24 4 24 6 24 11 24 _ _ = _ _ = m.c.m de 8, 6 y 4 = 24
10. NÚMEROS FRACCIONARIOS Multiplicación de Fracciones Para multiplicar fracciones, se multiplican los numeradores y el resultado se coloca como numerador; y se multiplican los denominadores y el resultado se coloca como denominador. 1 4 7 8 1 6 7 192 * * = 1 5 3 7 3 8 * * 9 280 = Pasamos a División de Fracciones (Antes Quebrados)
11. NÚMEROS FRACCIONARIOS División de Fracciones                                                                                                                                                                                                                    Para dividir fracciones, se multiplica la primera fracción por las fracciones inversas de las demás. Una fracción es inversa de otra cuando sus cantidades cambian de lugar ( 3/5 es inversa de 5/3 ).
12. NÚMEROS FRACCIONARIOS Simplificar Fracciones Para simplificar fracciones hay que averiguar el m.c.d. (máximo común divisor) del numerador y del denominador. Posteriormente, el numerador y denominador se divide entre el m.c.d. y el resultado será la fracción irreducible.
13. NÚMEROS FRACCIONARIOS Problema Se compró una lavadora por 360 €. El pago se realizó en tres plazos. El 1º de 1/5 del total; el 2º, 1/3 del total; y en el 3º, el resto. ¿Cuánto se pagó en el 3º plazo? 1 de 360; 3 360 * 1 5 = 72 € 360 * 1 3 = 120 € 1 de 360; 5 72 + 120 =192; 360 – 192 = 168 Solución: 168 € 1º plazo 2º plazo

Historia
Las primera fracciones fueron utilizadas para representar «partes de un entero», por medio del concepto de recíproco de un número entero. Esto equivale a considerar fracciones como: un medio, un tercio, un cuarto, etc. Posteriormente, se introdujo la «raya horizontal» de separación entre numerador y denominador, y el numerador dejó de restringirse al número uno solamente, dando origen a las llamadas fracciones vulgares o comunes. Finalmente, se introduce como notación definitiva las «fracciones decimales», o simplemente números decimales (o decimal), en donde el denominador se escribe como una potencia de diez.^[2]

Representación de las fracciones

Las fracciones e componen de: numerador, denominador y línea divisoria entre ambos (horizontal u oblícua). El denominador representa las cantidad de partes en que se ha fraccionado la unidad, y el numerador la cantidad de éstas consideradas.

Representación gráfica

Suelen utilizarse círculos o rectángulos (los cuales representan la unidad) divididos en tantas partes como indique el denominador, y se colorean (u omiten) tantas de estas partes como indique el numerador.

Representación analítica

La expresión genérica representa una división algebraica, por lo que el divisor debe ser distinto de cero, esto es: b ≠ 0; en una fracción común, a y b son números enteros (con b ≠ 0), y el cociente da por resultado un número racional, es decir, que una fracción común representa un número racional, por lo que las fracciones comunes heredan todas las propiedades matemáticas de los racionales.

• Convenciones:
  • en una fracción a/b, el denominador b se lee como número ordinal (ejemplos: 1/4 se lee «un cuarto», 3/5 se lee «tres quintos»);
  • una fracción negativa se escribe con el signo menos delante de la fracción (ejemplos: -1/4 o 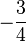; pero no 3/-4);
  • una fracción genérica a/b representa el producto de a por el recíproco multiplicativo de b, de tal modo que a/b = a • 1/b; si tanto a como b son números negativos ( − a / − b), el producto es positivo, por lo que se escribe: a/b;
  • toda expresión matemática escrita en esta forma (con b ≠ 0) recibe el nombre de fracción;

Ejemplos

• ; 3/4 ; ³/₄ ; (¾) ; fracción tres cuartos: numerador 3 y denominador 4, representa al número decimal 0.75;
• ; fracción: numerador x² y denominador (x+3)(x-3), el valor decimal dependerá del valor de la variable x.

Clasificación de fracciones

Cronología ^[3]

Año	Acontecimiento
1800 a.C.	Los babilonios utilizan fracciones.
1650	Los egipcios hacen uso de fracciones de unidad
100 d.C.	Los chinos inventan un sistema que permite calcular con fracciones.
1202	Leonardo de Pisa (Fibonacci) difunde la notación de fracción con barra.
1585	Simon Stevin expone una teoría sobre las fracciones decimales
1700	Uso generalizado de la línea fraccionaria.

Existen diversas formas para clasificar las fracciones, entre ellas están las siguientes:

• Según la relación entre el numerador y el denominador:
  • Fracción propia: fracción que tiene su denominador mayor que su numerador: ⅓, ⅜, ¾…
  • Fracción impropia: fracción en donde el numerador es mayor que el denominador: ¹³/₆, ¹⁸/₈, ⁵/₂…
• Según la relación entre los denominadores:
  • Fracción homogénea: fracciones que tienen el mismo denominador: ¼ y ¾
  • Fracción heterogénea: fracciones que tienen diferentes denominadores: ¼ y ⅔
• Según la relación entre el numerador y el denominador:
  • Fracción reducible: fracción en la que el numerador y el denominador no son primos entre sí y puede ser simplificada: ⁶/₁₂
  • Fracción irreducible: fracción en la que el numerador y el denominador son primos entre sí, y, por tanto, no puede ser simplificada: ½
• Otras clasificaciones:
  • Fracción unitaria: fracción común de numerador 1.
  • Fracción egipcia: sistema de representación de las fracciones en el Antiguo Egipto en el que cada fracción se expresa como suma de fracciones unitarias.
  • Fracción aparente o entera: fracción que representa cualquier número perteneciente al conjunto de los enteros: ³/₃=1, ¹⅔=4…

Ejemplo de fraccción aparente.

• • Fracción equivalente: la que tiene el mismo valor que otra dada: 1/2 = 2/4 = 4/8 = 50/100.
  • Fracción decimal: fracción cuyo denominador es una potencia de diez. También puede ser una fracción expresada en base 10, en contraposición con las fracciones binarias y demás, que están expresadas en otros sistemas de numeración.
  • Fracción mixta: suma de un entero y una fracción propia. Las fracciones mixtas se pueden expresar como fracciones impropias: 3¼
  • Una fracción irracional es, dado que todas las fracciones deben poder ser expresadas como fracciones vulgares, una término autocontradictorio. Un número irracional es, por definición, no racional, es decir, no puede ser expresado como una fracción vulgar.
  • Una fracción continua es una expresión como ésta:

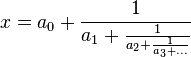
donde los a_i son enteros positivos.

• • Fracción compuesta: fracción cuyo numerador o denominador (o los dos) contiene a su vez fracciones.
  • Fracción parcial: la que puede usarse para descomponer una función racional.
  • Fracción como razón: Sirve a la pregunta ¿en qué relación están?, ya que pone de manifiesto la relación que mantienen un par de números que pueden provenir de una comparación.
  • Cuerpo de cocientes: Diversas fracciones pueden tener el mismo valor (llamadas fracciones equivalentes), y el conjunto de todas las fracciones equivalentes se denomina número racional.

Fracción de una cantidad

Si queremos dividir una cantidad en varias partes e indicar un número de esas partes, podemos hacerlo mediante fracciones, dividiendo la cantidad por el denominador y multiplicando el resultado por el numerador. Así, si queremos indicar ¾ (tres cuartos, o tres cuartas partes) de 453, hay que dividir 453 entre el denominador (en este caso, 4) y multiplicar el resultado por el numerador (en este caso, 3). El número obtenido es la fracción que queremos indicar.

Operaciones con fracciones

Amplificación de fracciones

Véase también: Amplificación y simplificación de fracciones

La amplificación de una fracción consiste en multiplicar el numerador y el denominador por un mismo número entero. De la misma manera, la simplificación de una fracción consiste en dividir el numerador y denominador entre un mismo número entero, que generalmente será uno de sus factores comunes. En ambos casos, se obtiene una fracción equivalente.
Ejemplos:

• (En esta amplificación de la fracción ⅔, se multiplica numerador y denominador por 4)
• (Aquí se simplifica 10/25 a ⅖ dividiendo numerador y denominador entre 5)

Comparación de fracciones

Véase también: Comparación de fracciones

La comparación de dos fracciones se utiliza para comprobar cuál es mayor. Existen varios métodos:

1. El método general consiste en amplificar las dos fracciones de modo que tengan el mismo denominador (por ejemplo, que tengan el mínimo común múltiplo (MCM) de las fracciones originales.
   • Por ejemplo, para y , el MCM de 12 y 8 es 24, por lo que bastaría con multiplicar amplificar la primera fracción en un factor de 2 y la segunda en un factor de 3. Se obtiene , que es mayor que
2. Si el numerador de las dos fracciones es el mismo, la fracción con el menor denominador es mayor que la otra. Esto es bastante natural: si se tienen dos tartas iguales, una para repartir entre más personas que la otra, la que se reparta entre menos personas estará partida en porciones más grandes.
3. Si el denominador de las dos fracciones es el mismo, la fracción con el mayor numerador es mayor que la otra.

Suma y resta de fracciones

Para sumar o restar fracciones, hay dos casos:

Tienen el mismo denominador

Entonces se suman o se restan los numeradores y se deja el denominador común.

• Ejemplo 1:

Es posible que el resultado se pueda simplificar.

• Ejemplo 2:

Tienen distinto denominador

Entonces, hay que amplificar las fracciones para que tengan el mismo denominador y luego sumar.

• Fórmula típica la suma:
• Fórmula típica para la resta:
• Ejemplo 1:

Observación: En realidad, no hace falta amplificar las fracciones de modo que el denominador resultante sea el producto de los denominadores de las fracciones iniciales. Basta con tomar el Mínimo común múltiplo de los denominadores:

• Fórmula para la suma:
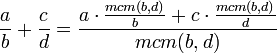
• Fórmula para la resta:
• Ejemplo 2:

Al final de la operación, puede que haga falta realizar otra simplificación.

Producto y cociente de fracciones

Para multiplicar dos fracciones, basta multiplicar los numeradores por una parte y los denominadores por otra:

• Fórmula para el producto:
• Ejemplo:

En el cociente de fracciones, el numerador de la fracción resultante es el producto del numerador de la fracción dividendo por el denominador de la fracción divisor, mientras que el denominador es igual al denominador de la fracción dividendo multiplicado por el numerador de la fracción divisor. Otra manera de imaginarlo es que dividir entre un número es lo mismo que multiplicar por el inverso de ese número, por lo que el cociente entre dos fracciones es igual al producto de la primera fracción por el inverso de la segunda: